Spatial indexing is the process of categorizing objects based on their physical position within a two-dimensional or three-dimensional space.  This report describes three spatial indexing structures (linear lists, quad trees, and k-d trees), and determines which should be used based on speed and ease of implementation.

Linear lists are simple to implement, but theoretically they are the slowest.  Quad trees and k-d trees (also known as partition trees) use more memory and are harder to implement than linear lists, but theoretically they have faster search times.

In practical tests, inserting an object into a partition tree was slower than inserting an object into a linear list.  The same held true for deletion, but the differences were not substantial.  For large searches, the linear list was the fastest spatial indexing structure; while the k-d tree was fastest for small areas (less than forty percent of the world).  The quad tree was the slowest structure for searching in all cases.

Many applications are required to display maps or schematics to users.  Spatial indexing structures are used to store this information and display it to users.  This report will focus on two dimentional-interactive spatial indexing structures.

Objects in a system can be divided into three categories: static objects, stationary objects, and moving objects.  Static objects, such as never move or change state.  Stationary objects never move, but may need to be redrawn to show a change in state.  Finally periodically change position.

Spatial indexing is the process of categorizing objects based on their physical position in a two-dimensional or three-dimensional space.  Based on the types of objects in the system, the spatial indexing method used must be able to support position changes, insertions, deletions, and range searches.  Range searches are used when updating or drawing the screen, and involve searching for a set of objects that intersect with a given rectangle. Position changes can be implemented as a deletion followed by an insertion. Thus, testing insertions, deletions, and range searches will provide insight into the efficiency of the data structure.  Since range searching is performed most frequently, the results of this operation are the most important.

This report will describe three spatial indexing methods, and determine which should be used for the SO window based on speed and ease of implementation.  Linear lists, quad trees, and k-d trees will be evaluated.

A linear list is the simplest data structure that can be used for spatial indexing.  An unordered linked list is used to store each object and its bounding rectangle.

To insert an object into a linear list, a new node containing the object and its bounding rectangle is first created.  This node is then appended to the end of the linked list. Since order does not matter, insertion can be performed in O(1) time.

Deletion can be implemented by searching the list for the given object and removing its node.  Because the entire list must be searched, deletion takes O(n); time where n is the number of objects.

Because nothing is known about the order of the objects in the list, a range search requires that every rectangle be tested against the search rectangle.  This means that every search requires O(n) comparisons.

A quad tree belongs to a class of spatial indexing structures known as partition trees. Partition trees divide the available space (known as the world) into several rectangles called regions. These regions are placed into a tree as nodes, and can be further divided using recursion. A quad tree divides the world into four, equally sized regions called quadrants.

The insertion, deletion, and range searching operations each depend on finding the set of regions that intersect with a given rectangle.  Recursion is used to generate a list of regions that intersect with the search rectangle.  Entire subtrees can be skipped if the rectangle does not intersect with them.  For example, if looking for rectangle D in Figure 1, subtrees 1, 2, and 4 could be skipped on the first iteration of the algorithm.

To insert into a quad tree, the bounding rectangle of the object is first calculated.  The object is then added to each intersecting region obtained from the above algorithm.

To delete, a list of regions that intersect the given rectangle is found using the algorithm above.  The object is then removed from each of these regions.

A list of regions that intersect the range is calculated. Objects contained in each region are extracted, and appended to a results list.  Finally, the results list is sorted, and duplicates are removed.

In the worst case, a quad tree is slower than a linear list.  This case occurs when searching the entire world.  If there are n objects, and the world is D levels deep, it would take approximately O(n*d) comparisons to create a list of unique intersecting objects.  However, assuming an even distribution and smaller search size, the expected number of comparisons for each operation is  O(root(n)*k) (where n is the number of objects and k is the number of regions) (source: Michael Goodrich and Roberto Tamassia, Data Structures and Algorithms in JAVA, John Wiley & Sons, (1998) 598-603.)

Like a quad tree, a k-d tree is a partition tree. However, instead of dividing the world into four equal regions, the area is continually divided into two regions.  This allows the use of a well understood data structure - the binary tree.  Static k-d trees divide each region so that an equal number of objects are on each side of the division.  This means the tree will be balanced, and allows for very fast range searching.  Unfortunately, this does not work very well when insertion and deletion are required.  A dynamic k-d tree recursively divides each area into two equally sized sub regions.  Although this does not guarantee a balanced tree, it works well for evenly distributed objects.

The insertion algorithm for a k-d tree is similar to the insertion algorithm for a quad tree.  First, the bounding rectangle of the object is calculated. Using a recursive algorithm, the object is added to each external node that intersects the bounding rectangle.  If the threshold (the maximum number of objects per region) has been reached, the region is split along the longest side.

To delete, a list of external nodes that intersect with the object's bounding rectangle is calculated using the range search algorithm.  The object is then removed from each of these regions.

A simple recursive algorithm can be used to find all objects that intersect with a given range.  If the range does not intersect with the node, an empty list is returned.  If the node is external, a sorted list of objects is returned. Otherwise, recursion is used to calculate the list of objects for each child.  These lists are merged and returned.

In a k-d tree, the running time for insertion, deletion, and range searching depends on how efficiently the list of regions, which intersect a given range, can be calculated.  Assuming the tree is balanced, the worse case would occur when a full search is performed. Since every node in the tree must be visited, and the height of the tree is log(n), the runtime would be O(n*log(n)).  The expected search time in a balanced k-d tree is  O(k + 2*root(n)) where n is the number of objects, and k is the number of results. (Source: Nguyen, DuPrie, and Zografou, A Multidimensional Binary Search Tree, 1998, http://www.stsci.edu/stsci/meetings/adassVII/nguyend.html)

To test insertion, a driver was created to insert a given number of random objects into each spatial partition structure.  This test was repeated several times, and the average runtimes recorded in the following graph: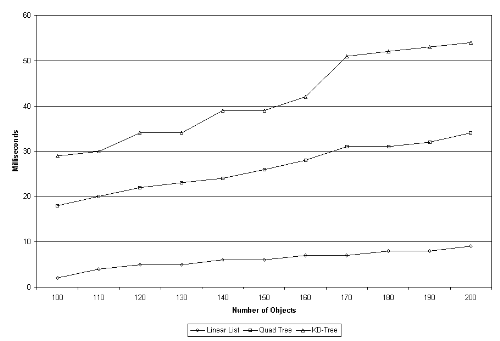

As expected, the linear list is by far the fastest structure for insertion.  It takes a constant amount of time for each insertion regardless of the number of objects currently in the structure.

It takes about ten times longer to form the initial quad tree, but after this, it takes a constant amount of time to insert each object.  The insertion time per object is approximately equal to the insertion time in a linear list.

Finally, the k-d tree takes about fifteen times longer to create than the linear list. But, unlike the quad tree, it does not become linear right away. Instead, it steps when each threshold is reached. If objects continually move along the same path, as they do in the train control system, insertion time is similar to the linear list.

To test deletion, the driver for insertion was modified to measure the average time it takes to remove all objects from a full spatial indexing structure.  The test was run several times, and the average runtimes recorded in the following graph: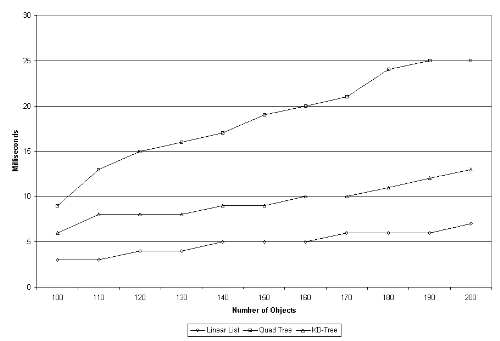

Deletion is similar for all three spatial indexing structures. It takes a constant amount of time to remove each object.

A k-d tree has a fixed maximum number of objects per node, while in concentrated areas, a quad tree node may have many objects per node.  This means longer lists must be searched in the quad tree, and consequently deletion is slightly slower.

To test searching, a driver was created to fill each structure with five hundred objects.  The total time to perform five randomly located searches of each size was measured and recorded in Figure 7.

When the area being searched is small (less than 40% of the world size) the k-d tree is fastest. However, as the size of the search area increases, the search time increases exponentially.  In contrast, the search time using the linear list grows at a constant rate, and is thus substantially faster for searching large areas.  In all cases, the quad tree is the slowest structure for searching.

The k-d tree and quad tree are slower for larger searches because duplicates must be removed from the list. These are removed by sorting the list and comparing all adjacent objects.  If duplicates are allowed, searches in the k-d tree and quad tree are much faster, but are still slower than the linear list for full world searches.

The following table summarizes the expected running times and space requirements for each of the spatial indexing structures analyzed.

The following table summarizes the relative experimental run times of each data structure.

• Implementing and maintaining a linear list, quad tree, or a k-d tree should be straightforward due to numerous references available.
• When there are only a small number of objects (less than 200), a linear list is the fastest structure for all operations.
• Inserting objects into and deleting objects from a pre-existing indexing structure takes approximately the same time regardless of the structure used.
• Although the linear list was the fastest structure for searching large areas, it was significantly slower than both the k-d tree and quad tree for searching small areas.  As indicated in the introduction, small range searches are the most common operation, and it is important that an efficient algorithm be used.

• The quad tree that is is adequate for small, simple schematics.  However, its poor performance may become an issue for larger interactive systems.
• Since k-d trees and linear lists complement each other (linear lists work well for large searches while k-d trees work well for small searches), a hybrid data structure was considered.  Although a hybrid would likely be more efficient, it would also be harder to maintain and debug.  Thus, a standard spatial indexing method should be used.

Adali, Sibel. "Knowledge Systems Lecture Slides." 1998.  http://www.cs.rpi.edu/~sibel/4962/class16/tsld014.htm (2000/08/27)

Brabec and Samet. "Spatial Index Demos." 1999. http://www.cs.umd.edu/~brabec/quadtree  (2000/08/20)

Goodrich and Tamassia. Data Structures and Algorithms in JAVA. New York: John Wiley & Sons, 1998.

Nguyen, DuPrie, and Zografou. "A Multidimensional Binary Search Tree." 1998. http://www.stsci.edu/stsci/meetings/adassVII/nguyend.html (2000/08/27)

Kelly, Steve - GUI Team Leader (Steve.Kelly -{@}- tas.alcatel.ca)

Pretti, J.P. Professor CS240 University of Waterloo (jpretti -{@}- uwaterloo.ca)

The following is the source code and MSVC++ project I used to do my tests. I provide no gaurentee on this code, and you may download and compile it at your own risk. This code is not to be used in any application without prior approvial by me.

Click to download spatial.zip

Click read about MetLife experience